Plush Wars

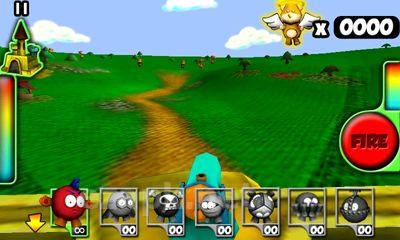
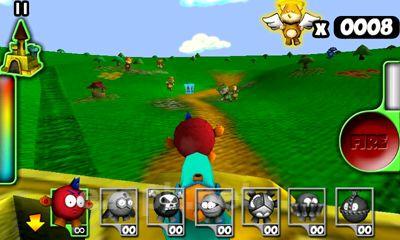
Welcome to Plush Wars, where your mission is to protect the castle of Princess Plushlandia and the princess herself from an invasion of plush zombies. In this plush country, the only real weapon is a gun, while everything else, including ammunition, is made of plush material. From all directions, you will be faced with teddy bears and doggies that have been turned into zombies, most likely due to mischievous children tearing off their button eyes, paws, and heads. Your weapon of choice is a gun loaded with plush bullets. Your first step is to select your target, and then press the button to fire.<|endoftext|><|endoftext|> # 2015 AMC 10A Problems/Problem 1. ## Contents. 1 Problem 2 Solution 3 Video Solution 4 See Also ## Problem What is the value of \[2-4+6-8+10-12+14-16+18-20?\] $\textbf{(A)}\ -10\qquad\textbf{(B)}\ -2\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 2\qquad\textbf{(E)}\ 10$ ## Solution. We can rearrange the terms to get \[2+6+10+14+18-4-8-12-16-20.\] Now, we can pair up the terms to get \[(2-2)+(6-4)+(10-8)+(14-12)+(18-16)-20.\] Simplifying, we get \[0+2+2+2+2-20=10-20=\boxed{\textbf{(A)}\ -10}.\] ## Video Solution. https://youtu.be/8-3XeJXm-qE ~savannahsolver <|endoftext|>## Mathematical Forums ## Category: High School Olympiads ## Topic: Inequality ## Views: 338 ## [enter: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Let $a,b,c>0$. Prove that $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b+c)$ ## [enter: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] By AM-GM have:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ and similar we get:$\sum_{cyc}\frac{a^2}{b}+a+b\ge3(a+b+c)$ $\implies$ $\sum_{cyc}\frac{a^2