Pixelo

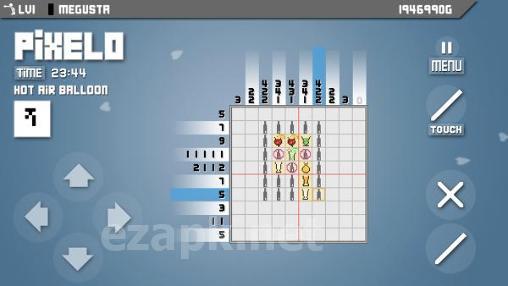
Pixelo is an Android game where you use your logic and imagination to solve puzzles by coloring in tiles on the screen to create a picture. The grid can range from 5x5 to 20x20 tiles and each column and row has numbers indicating how many tiles need to be filled in. The colored groups of tiles must be separated by at least one blank tile. With over 500 puzzles, great graphics, simple controls, high scores, and absorbing gameplay, Pixelo is a must-try game.<|endoftext|><|endoftext|> # 2015 AMC 10A Problems/Problem 1. ## Contents. 1 Problem 2 Solution 3 Video Solution 4 See Also ## Problem What is the value of \[2-4+6-8+10-12+14-16+18-20+22?\] $\textbf{(A)}\ -110\qquad\textbf{(B)}\ -44\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 22\qquad\textbf{(E)}\ 110$ ## Solution. We can rearrange the terms to get \[2+6+10+14+18+22-4-8-12-16-20.\] Now, we can pair up the terms to get \[(2+22)+(6+18)+(10+14)-4-8-12-16-20.\] Simplifying, we get \[24+24+24-60=\boxed{\textbf{(C)}\ 0}.\] ## Video Solution. https://youtu.be/8zQNG5RZuJw ~savannahsolver <|endoftext|>## Mathematical Forums ## Category: High School Olympiads ## Topic: Inequality ## Views: 338 ## [enter: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Let $a,b,c>0$. Prove that $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b+c)$ ## [enter: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] By AM-GM have $3\sqrt[3]{abc}\ge a+b+c$ and by Cauchy-Schwarz have $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\ge\frac{(a+b+c)^2}{a+b+c}=a+b+c$ hence $LHS\ge2(a+b+c)$ ## [math-user1, num_likes=1] [quote=math-user2]By