Legend of Minerva

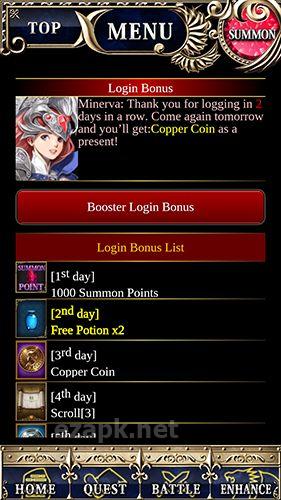
Transform yourself into a true knight and conquer malevolent forces in the fantasy-themed online RPG game - Legend of Minerva. Highlights: Explore over 1000 vibrant maps, invite friends for bonuses, engage in epic battles against bosses, form guilds, and immerse yourself in an exceptional storyline.<|endoftext|><|endoftext|> # 2015 AMC 10B Problems/Problem 1. ## Contents. 1 Problem 2 Solution 3 Video Solution 4 See Also ## Problem What is the value of $2+4+6+8+10+12+14+16+18+20$? $\textbf{(A)}\ 90\qquad\textbf{(B)}\ 100\qquad\textbf{(C)}\ 110\qquad\textbf{(D)}\ 120\qquad\textbf{(E)}\ 130$ ## Solution. We can pair the numbers up as follows: $(2+20)+(4+18)+(6+16)+(8+14)+(10+12)$. Each pair adds up to $22$, and there are $5$ pairs, so the sum is $22 \cdot 5 = \boxed{\textbf{(B)}\ 100}$. ## Video Solution. https://youtu.be/8WrdYLw9_ns ~savannahsolver <|endoftext|>## Mathematical Forums ## Category: High School Olympiads ## Topic: Inequality ## Views: 338 ## [enter: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Let $a,b,c$ be positive real numbers such that $a+b+c=3$. Prove that $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+3\geq 2(ab+bc+ca)$ ## [enter: math-user2, num_posts=467, num_likes_received=180] ## [math-user2, num_likes=0] By AM-GM, $ab+bc+ca\le\frac{\left(a+b+c\right)^2}{3}=3$. So we need to prove $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\ge3$. By AM-GM, $\frac{a}{b}+\frac{a}{b}+\frac{b}{c}\ge3\sqrt[3]{\frac{a^2}{bc}}=3\sqrt[3]{\frac{a^3}{abc}}=3\sqrt[3]{\frac{a^3}{abc}\cdot\frac{b^3}{abc}\cdot\frac{c^3}{abc}}=3$. Summing cyclically gives the desired result. ## [enter: math-user3, num_posts=545, num